Cómo amañar bien unas elecciones

Breve explicación de cómo unas listas abiertas, algo de conocimiento de combinatoria y alguna conexión con la mafia te puede asegurar el éxito electoral

Mar 31, 2022

Si es usted un mafioso y quiere amañar unas elecciones más o menos decentes lo va a tener difícil. Modificar los votos una vez introducidos es prácticamente imposible en una democracia occidental, y votar varias veces (o votar siendo menor) no es un opción dado lo riguroso del censo.

Lo primero que se ocurre a alguien entonces es usar la fuerza bruta: vas casa por casa amenazando a todo Dios con darle una paliza si no introducen tu nombre en la papeleta, pero aquí hay un problema importante:

Un tirano no puede ser arbitrariamente violento. Un poco sí, porque siempre existe un pequeño óptimo de locura que puede venirle bien a cualquiera, pero el voto es secreto. Eso significa que si no ganas y te dispones a aplicar tu castigo vas a castigar a culpables (de no votarte) e inocentes por igual, y por lo general esto no es una buena estrategia. El incentivo a obedecerte la siguiente vez va a ser nulo.

How to Rig an Election : Cheeseman, Nic, Klaas, Brian, Josdal, Matthew: Amazon.es: Libros

Uno podría pensar que el soborno sería una mejor estrategia, podrías prometer un dinero a un grupo de gente si ganas, pero dejando de lado que sin el ingrediente del miedo la probabilidad de chivato aumenta exponencialmente; esto nos saldría muy caro (y estaríamos pagando, de nuevo, a culpables e inocentes por igual). ¿Cómo lo solucionamos? Pues aquí dejo un truco útil siempre que se cumplan las siguientes condiciones:

Las listas deben ser abiertas
Los resultados han de ser públicos (aunque sigan siendo anónimos, uno debe poder ver qué papeletas se han introducido en cada urna/distrito). También sirve con poder estar presente en el recuento de las mesas, aunque complicaría la operativa no afecta en nada al método.
Debes tener alguna conexión con la mafia o tener mucho dinero. Tú eliges si palo o zanahoria; aquí no tendremos el mismo problema de antes

El método en cuestión

Por simplicidad, supongamos un distrito electoral con 5000 personas llamadas a votar (de las cuales irán ~2/3). Pongamos que hay 15 candidatos (y no tienes compinches, “en tu partido sólo estás tú”, digamos que eres el primero que aparece en la papeleta, el #1) y cada persona vota a cuatro, así existen 364 “formas de votar” al candidato #1 (1-2-3-4, 1-2-3-5… 1-3-4-(12)…1-4-5-7…, el orden de los números da igual, 1-2-3-4=2-4-3-1=3-1-2-4=…):

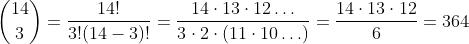
“Fijamos” el candidato #1 y queda una combinación de (15-1) diputados de los que puedes elegir (4-1)

Cuando acaben las elecciones se publicarán las papeletas, así que no sólo sabrás cuántos votos ha recibido cada diputado sino junto a quienes ha sido votado. Ahora es tan sencillo como “darle una visita” al panadero, al de la pizzería, y a 362 personas más y decirles:

Mire usted, cuando publiquen las papeletas quiero que aparezcan los diputados 1, 3 ,5 y 14. Al vecino le dices que quieres 1-2-4-(10), y a cada visitante le das un número distinto. De ti depende cómo seguir la frase, puedes decirle que su hijo es muy majo y sería una pena que le pasase algo o que es una pena que siendo tan listo no le de para estudiar y quizás puedas echar una mano.

Tan sólo resta mirar las papeletas y ver si efectivamente los números que has pedido están en la lista, quizás el votante no haya sucumbido a tus amenazas/sobornos pero otra persona haya votado justo su número por pura casualidad, pero tampoco te importa mucho (la probabilidad de que eso ocurra es, asumiendo que todos los candidatos tienen la misma probabilidad -¡MENTIRAAAAA!-, de 1/1365, y de que pase dos veces es de (1/1365)·(1/1364)=1/1861860).

Efectividad

¿Cómo de efectivo es este método? En primer lugar es más seguro que los métodos mentados en la introducción, pues los incentivos de los votantes están mejor alineados al saber que el castigo/recompensa no será arbitrario. Por otro lado hemos dicho que acudirán a votar ~2/3 de las 5000 posibles votantes, así que habrá ~3330 votos, de los cuales tu puedes controlar 364 (aproximadamente el 10%). Hay otro factor a tener en cuenta y es que quizás no quieres que nadie vote a cierto candidato aunque te vote a ti también, lo cual reducirá el número de posibilidades. También es cierto que estos números son muy susceptibles al número de diputados, si en vez de 15 tuviéramos 17 tendríamos control sobre 680 votos, aproximadamente el doble que antes. No sucede lo mismo con el número de elecciones que puedes hacer, el óptimo es la mitad de diputados y las posibilidades se reducen contra más te alejes de ahí en cualquier dirección.

Caso práctico

En 2019 se presentaron en la provincia de Albacete 21 (posibles) diputados1. Albacete es una provincia con 300k electores y 517 mesas2. Hubo 216.000 votos válidos (69%)3 así que nos quedamos a 418 votos/mesa. ¿Cuántas combinaciones podemos hacer teniendo un único mafioso en las listas? 20 sobre 2, es decir 190 de los 418 votos. Aún asumiendo que no quieres incluir al candidato que más posibilidades tiene de ganar te quedan (19 sobre 2)=171 votos. Ver que si en las papeletas para el senado en vez de 3 pudiéramos marcar 4 diputados entonces tendríamos “control” sobre (19 sobre 3)=969 votos con 418 votos/mesa. Obviamente aquí “control” se refiere únicamente a la combinatoria, ¡aún te queda convencer a la peña!

En cierto sentido lo que más me gusta de este método es que es más útil contra más se acerquen las elecciones al ideal democrático de muchos, es decir, listas abiertas y gran cantidad de elecciones. Obviamente en sistemas en los que puedas coaccionar o sobornar a tanta gente de forma impune son tremendamente susceptibles a formas más clásicas de pucherazo (si os gustan estos temas puedo resumir este paper4 sobre cómo efectivamente la mafia italiana amañaba elecciones), así que niños no lo intentéis en casa.

De nuevo, si estas cosas os parecen interesantes podemos ir intercalándolas con los resúmenes de libros de filosofía, que son bastante más pesados.

Laissez passer

Discussion about this post